Appendix B: Practice

This appendix aims to give you some challenging and interesting exercises to test and solidify your understanding of the main topics from this book. It's a good idea to try out the exercises yourself—in an actual code editor!—instead of skipping straight to the solutions at the end. No cheating!

These exercises don't have a specific right answer that you have to get exactly. Your approach may differ some (or a lot!) from the solutions presented, and that's OK.

There's no judging you on how you write your code. My hope is that you come away from this book feeling confident that you can tackle these sorts of coding tasks built on a strong foundation of knowledge. That's the only objective, here. If you're happy with your code, I am, too!

Buckets of Marbles

Remember Figure 2 from back in Chapter 2?

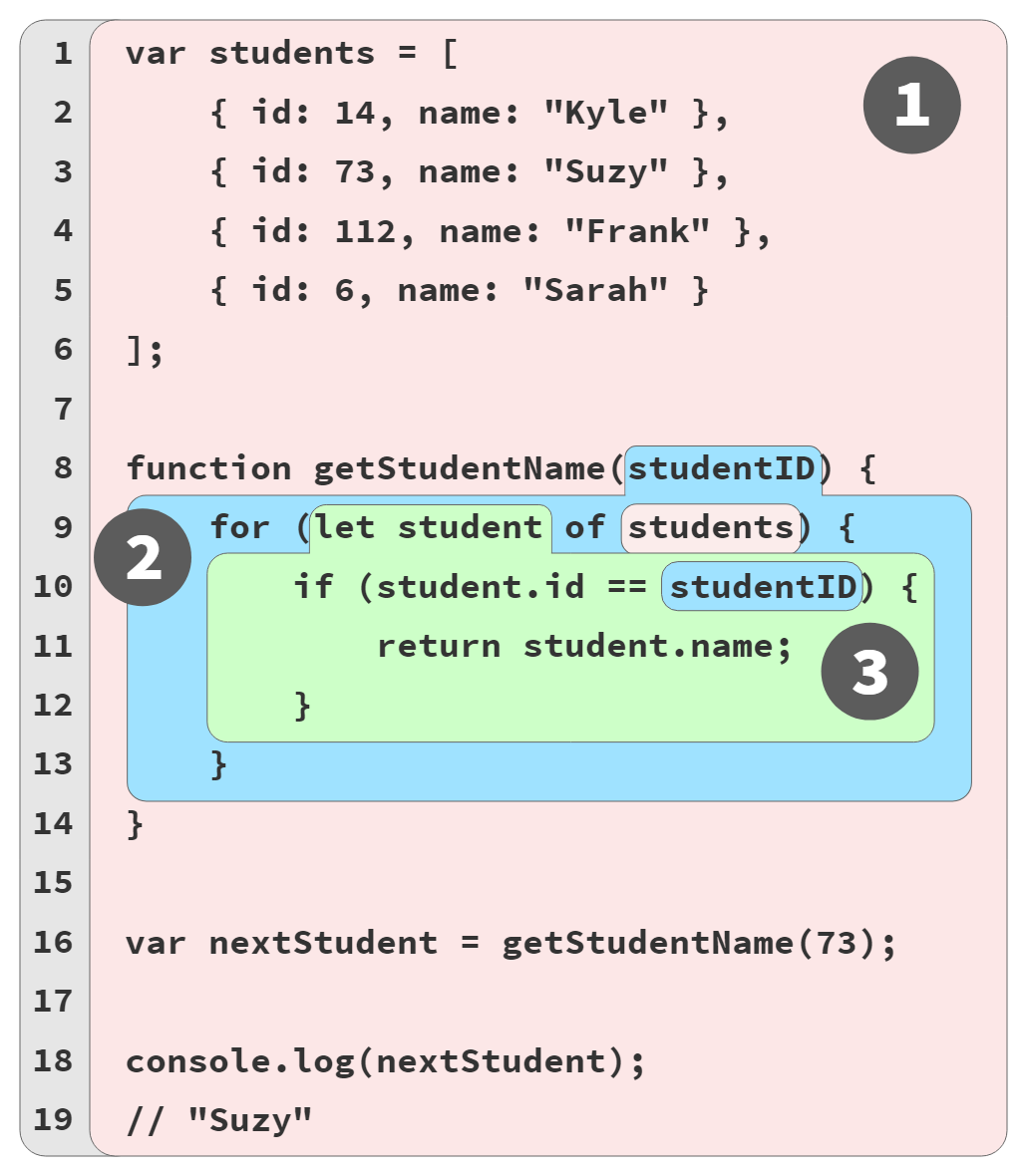
Colored Scope Bubbles
Fig. 2 (Ch. 2): Colored Scope Bubbles

This exercise asks you to write a program—any program!—that contains nested functions and block scopes, which satisfies these constraints:

  • If you color all the scopes (including the global scope!) different colors, you need at least six colors. Make sure to add a code comment labeling each scope with its color.

    BONUS: identify any implied scopes your code may have.

  • Each scope has at least one identifier.

  • Contains at least two function scopes and at least two block scopes.

  • At least one variable from an outer scope must be shadowed by a nested scope variable (see Chapter 3).

  • At least one variable reference must resolve to a variable declaration at least two levels higher in the scope chain.

TIP:
You can just write junk foo/bar/baz-type code for this exercise, but I suggest you try to come up with some sort of non-trivial real'ish code that at least does something kind of reasonable.

Try the exercise for yourself, then check out the suggested solution at the end of this appendix.

Closure (PART 1)

Let's first practice closure with some common computer-math operations: determining if a value is prime (has no divisors other than 1 and itself), and generating a list of prime factors (divisors) for a given number.

For example:

isPrime(11); // true
isPrime(12); // false
factorize(11); // [ 11 ]
factorize(12); // [ 3, 2, 2 ] --> 3*2*2=12

Here's an implementation of isPrime(..), adapted from the Math.js library: mathjsisprime

function isPrime(v) {
if (v <= 3) {
return v > 1;
}
if (v % 2 == 0 || v % 3 == 0) {
return false;
}
var vSqrt = Math.sqrt(v);
for (let i = 5; i <= vSqrt; i += 6) {
if (v % i == 0 || v % (i + 2) == 0) {
return false;
}
}
return true;
}

And here's a somewhat basic implementation of factorize(..) (not to be confused with factorial(..) from Chapter 6):

function factorize(v) {
if (!isPrime(v)) {
let i = Math.floor(Math.sqrt(v));
while (v % i != 0) {
i--;
}
return [...factorize(i), ...factorize(v / i)];
}
return [v];
}
NOTE:
I call this basic because it's not optimized for performance. It's binary-recursive (which isn't tail-call optimizable), and it creates a lot of intermediate array copies. It also doesn't order the discovered factors in any way. There are many, many other algorithms for this task, but I wanted to use something short and roughly understandable for our exercise.

If you were to call isPrime(4327) multiple times in a program, you can see that it would go through all its dozens of comparison/computation steps every time. If you consider factorize(..), it's calling isPrime(..) many times as it computes the list of factors. And there's a good chance most of those calls are repeats. That's a lot of wasted work!

The first part of this exercise is to use closure to implement a cache to remember the results of isPrime(..), so that the primality (true or false) of a given number is only ever computed once. Hint: we already showed this sort of caching in Chapter 6 with factorial(..).

If you look at factorize(..), it's implemented with recursion, meaning it calls itself repeatedly. That again means we may likely see a lot of wasted calls to compute prime factors for the same number. So the second part of the exercise is to use the same closure cache technique for factorize(..).

Use separate closures for caching of isPrime(..) and factorize(..), rather than putting them inside a single scope.

Try the exercise for yourself, then check out the suggested solution at the end of this appendix.

A Word About Memory

I want to share a little quick note about this closure cache technique and the impacts it has on your application's performance.

We can see that in saving the repeated calls, we improve computation speed (in some cases, by a dramatic amount). But this usage of closure is making an explicit trade-off that you should be very aware of.

The trade-off is memory. We're essentially growing our cache (in memory) unboundedly. If the functions in question were called many millions of times with mostly unique inputs, we'd be chewing up a lot of memory. This can definitely be worth the expense, but only if we think it's likely we see repetition of common inputs so that we're taking advantage of the cache.

If most every call will have a unique input, and the cache is essentially never used to any benefit, this is an inappropriate technique to employ.

It also might be a good idea to have a more sophisticated caching approach, such as an LRU (least recently used) cache, that limits its size; as it runs up to the limit, an LRU evicts the values that are... well, least recently used!

The downside here is that LRU is quite non-trivial in its own right. You'll want to use a highly optimized implementation of LRU, and be keenly aware of all the trade-offs at play.

Closure (PART 2)

In this exercise, we're going to again practive closure by defining a toggle(..) utility that gives us a value toggler.

You will pass one or more values (as arguments) into toggle(..), and get back a function. That returned function will alternate/rotate between all the passed-in values in order, one at a time, as it's called repeatedly.

function toggle(/* .. */) {
// ..
}
var hello = toggle("hello");
var onOff = toggle("on", "off");
var speed = toggle("slow", "medium", "fast");
hello(); // "hello"
hello(); // "hello"
onOff(); // "on"
onOff(); // "off"
onOff(); // "on"
speed(); // "slow"
speed(); // "medium"
speed(); // "fast"
speed(); // "slow"

The corner case of passing in no values to toggle(..) is not very important; such a toggler instance could just always return undefined.

Try the exercise for yourself, then check out the suggested solution at the end of this appendix.

Closure (PART 3)

In this third and final exercise on closure, we're going to implement a basic calculator. The calculator() function will produce an instance of a calculator that maintains its own state, in the form of a function (calc(..), below):

function calculator() {
// ..
}
var calc = calculator();

Each time calc(..) is called, you'll pass in a single character that represents a keypress of a calculator button. To keep things more straightforward, we'll restrict our calculator to supporting entering only digits (0-9), arithmetic operations (+, -, *, /), and "=" to compute the operation. Operations are processed strictly in the order entered; there's no "( )" grouping or operator precedence.

We don't support entering decimals, but the divide operation can result in them. We don't support entering negative numbers, but the "-" operation can result in them. So, you should be able to produce any negative or decimal number by first entering an operation to compute it. You can then keep computing with that value.

The return of calc(..) calls should mimic what would be shown on a real calculator, like reflecting what was just pressed, or computing the total when pressing "=".

For example:

calc("4"); // 4
calc("+"); // +
calc("7"); // 7
calc("3"); // 3
calc("-"); // -
calc("2"); // 2
calc("="); // 75
calc("*"); // *
calc("4"); // 4
calc("="); // 300
calc("5"); // 5
calc("-"); // -
calc("5"); // 5
calc("="); // 0

Since this usage is a bit clumsy, here's a useCalc(..) helper, that runs the calculator with characters one at a time from a string, and computes the display each time:

function useCalc(calc, keys) {
return [...keys].reduce(function showDisplay(display, key) {
var ret = String(calc(key));
return display + (ret != "" && key == "=" ? "=" : "") + ret;
}, "");
}
useCalc(calc, "4+3="); // 4+3=7
useCalc(calc, "+9="); // +9=16
useCalc(calc, "*8="); // *5=128
useCalc(calc, "7*2*3="); // 7*2*3=42
useCalc(calc, "1/0="); // 1/0=ERR
useCalc(calc, "+3="); // +3=ERR
useCalc(calc, "51="); // 51

The most sensible usage of this useCalc(..) helper is to always have "=" be the last character entered.

Some of the formatting of the totals displayed by the calculator require special handling. I'm providing this formatTotal(..) function, which your calculator should use whenever it's going to return a current computed total (after an "=" is entered):

function formatTotal(display) {
if (Number.isFinite(display)) {
// constrain display to max 11 chars
let maxDigits = 11;
// reserve space for "e+" notation?
if (Math.abs(display) > 99999999999) {
maxDigits -= 6;
}
// reserve space for "-"?
if (display < 0) {
maxDigits--;
}
// whole number?
if (Number.isInteger(display)) {
display = display.toPrecision(maxDigits).replace(/\.0+$/, "");
}
// decimal
else {
// reserve space for "."
maxDigits--;
// reserve space for leading "0"?
if (Math.abs(display) >= 0 && Math.abs(display) < 1) {
maxDigits--;
}
display = display.toPrecision(maxDigits).replace(/0+$/, "");
}
} else {
display = "ERR";
}
return display;
}

Don't worry too much about how formatTotal(..) works. Most of its logic is a bunch of handling to limit the calculator display to 11 characters max, even if negatives, repeating decimals, or even "e+" exponential notation is required.

Again, don't get too mired in the mud around calculator-specific behavior. Focus on the memory of closure.

Try the exercise for yourself, then check out the suggested solution at the end of this appendix.

Modules

This exercise is to convert the calculator from Closure (PART 3) into a module.

We're not adding any additional functionality to the calculator, only changing its interface. Instead of calling a single function calc(..), we'll be calling specific methods on the public API for each "keypress" of our calculator. The outputs stay the same.

This module should be expressed as a classic module factory function called calculator(), instead of a singleton IIFE, so that multiple calculators can be created if desired.

The public API should include the following methods:

  • number(..) (input: the character/number "pressed")
  • plus()
  • minus()
  • mult()
  • div()
  • eq()

Usage would look like:

var calc = calculator();
calc.number("4"); // 4
calc.plus(); // +
calc.number("7"); // 7
calc.number("3"); // 3
calc.minus(); // -
calc.number("2"); // 2
calc.eq(); // 75

formatTotal(..) remains the same from that previous exercise. But the useCalc(..) helper needs to be adjusted to work with the module API:

function useCalc(calc, keys) {
var keyMappings = {
"+": "plus",
"-": "minus",
"*": "mult",
"/": "div",
"=": "eq",
};
return [...keys].reduce(function showDisplay(display, key) {
var fn = keyMappings[key] || "number";
var ret = String(calc[fn](key));
return display + (ret != "" && key == "=" ? "=" : "") + ret;
}, "");
}
useCalc(calc, "4+3="); // 4+3=7
useCalc(calc, "+9="); // +9=16
useCalc(calc, "*8="); // *5=128
useCalc(calc, "7*2*3="); // 7*2*3=42
useCalc(calc, "1/0="); // 1/0=ERR
useCalc(calc, "+3="); // +3=ERR
useCalc(calc, "51="); // 51

Try the exercise for yourself, then check out the suggested solution at the end of this appendix.

As you work on this exercise, also spend some time considering the pros/cons of representing the calculator as a module as opposed to the closure-function approach from the previous exercise.

BONUS: write out a few sentences explaining your thoughts.

BONUS #2: try converting your module to other module formats, including: UMD, CommonJS, and ESM (ES Modules).

Suggested Solutions

Hopefully you've tried out the exercises before you're reading this far. No cheating!

Remember, each suggested solution is just one of a bunch of different ways to approach the problems. They're not "the right answer," but they do illustrate a reasonable way to approach each exercise.

The most important benefit you can get from reading these suggested solutions is to compare them to your code and analyze why we each made similar or different choices. Don't get into too much bikeshedding; try to stay focused on the main topic rather than the small details.

Suggested: Buckets of Marbles

The Buckets of Marbles Exercise can be solved like this:

// RED(1)
const howMany = 100;
// Sieve of Eratosthenes
function findPrimes(howMany) {
// BLUE(2)
var sieve = Array(howMany).fill(true);
var max = Math.sqrt(howMany);
for (let i = 2; i < max; i++) {
// GREEN(3)
if (sieve[i]) {
// ORANGE(4)
let j = Math.pow(i, 2);
for (let k = j; k < howMany; k += i) {
// PURPLE(5)
sieve[k] = false;
}
}
}
return sieve
.map(function getPrime(flag, prime) {
// PINK(6)
if (flag) return prime;
return flag;
})
.filter(function onlyPrimes(v) {
// YELLOW(7)
return !!v;
})
.slice(1);
}
findPrimes(howMany);
// [
// 2, 3, 5, 7, 11, 13, 17,
// 19, 23, 29, 31, 37, 41,
// 43, 47, 53, 59, 61, 67,
// 71, 73, 79, 83, 89, 97
// ]

Suggested: Closure (PART 1)

The Closure Exercise (PART 1) for isPrime(..) and factorize(..), can be solved like this:

var isPrime = (function isPrime(v) {
var primes = {};
return function isPrime(v) {
if (v in primes) {
return primes[v];
}
if (v <= 3) {
return (primes[v] = v > 1);
}
if (v % 2 == 0 || v % 3 == 0) {
return (primes[v] = false);
}
let vSqrt = Math.sqrt(v);
for (let i = 5; i <= vSqrt; i += 6) {
if (v % i == 0 || v % (i + 2) == 0) {
return (primes[v] = false);
}
}
return (primes[v] = true);
};
})();
var factorize = (function factorize(v) {
var factors = {};
return function findFactors(v) {
if (v in factors) {
return factors[v];
}
if (!isPrime(v)) {
let i = Math.floor(Math.sqrt(v));
while (v % i != 0) {
i--;
}
return (factors[v] = [...findFactors(i), ...findFactors(v / i)]);
}
return (factors[v] = [v]);
};
})();

The general steps I used for each utility:

  1. Wrap an IIFE to define the scope for the cache variable to reside.

  2. In the underlying call, first check the cache, and if a result is already known, return.

  3. At each place where a return was happening originally, assign to the cache and just return the results of that assignment operation—this is a space savings trick mostly just for brevity in the book.

I also renamed the inner function from factorize(..) to findFactors(..). That's not technically necessary, but it helps it make clearer which function the recursive calls invoke.

Suggested: Closure (PART 2)

The Closure Exercise (PART 2) toggle(..) can be solved like this:

function toggle(...vals) {
var unset = {};
var cur = unset;
return function next() {
// save previous value back at
// the end of the list
if (cur != unset) {
vals.push(cur);
}
cur = vals.shift();
return cur;
};
}
var hello = toggle("hello");
var onOff = toggle("on", "off");
var speed = toggle("slow", "medium", "fast");
hello(); // "hello"
hello(); // "hello"
onOff(); // "on"
onOff(); // "off"
onOff(); // "on"
speed(); // "slow"
speed(); // "medium"
speed(); // "fast"
speed(); // "slow"

Suggested: Closure (PART 3)

The Closure Exercise (PART 3) calculator() can be solved like this:

// from earlier:
//
// function useCalc(..) { .. }
// function formatTotal(..) { .. }
function calculator() {
var currentTotal = 0;
var currentVal = "";
var currentOper = "=";
return pressKey;
// ********************
function pressKey(key) {
// number key?
if (/\d/.test(key)) {
currentVal += key;
return key;
}
// operator key?
else if (/[+*/-]/.test(key)) {
// multiple operations in a series?
if (currentOper != "=" && currentVal != "") {
// implied '=' keypress
pressKey("=");
} else if (currentVal != "") {
currentTotal = Number(currentVal);
}
currentOper = key;
currentVal = "";
return key;
}
// = key?
else if (key == "=" && currentOper != "=") {
currentTotal = op(currentTotal, currentOper, Number(currentVal));
currentOper = "=";
currentVal = "";
return formatTotal(currentTotal);
}
return "";
}
function op(val1, oper, val2) {
var ops = {
// NOTE: using arrow functions
// only for brevity in the book
"+": (v1, v2) => v1 + v2,
"-": (v1, v2) => v1 - v2,
"*": (v1, v2) => v1 * v2,
"/": (v1, v2) => v1 / v2,
};
return ops[oper](val1, val2);
}
}
var calc = calculator();
useCalc(calc, "4+3="); // 4+3=7
useCalc(calc, "+9="); // +9=16
useCalc(calc, "*8="); // *5=128
useCalc(calc, "7*2*3="); // 7*2*3=42
useCalc(calc, "1/0="); // 1/0=ERR
useCalc(calc, "+3="); // +3=ERR
useCalc(calc, "51="); // 51
NOTE:
Remember: this exercise is about closure. Don't focus too much on the actual mechanics of a calculator, but rather on whether you are properly remembering the calculator state across function calls.

Suggested: Modules

The Modules Exercise calculator() can be solved like this:

// from earlier:
//
// function useCalc(..) { .. }
// function formatTotal(..) { .. }
function calculator() {
var currentTotal = 0;
var currentVal = "";
var currentOper = "=";
var publicAPI = {
number,
eq,
plus() {
return operator("+");
},
minus() {
return operator("-");
},
mult() {
return operator("*");
},
div() {
return operator("/");
},
};
return publicAPI;
// ********************
function number(key) {
// number key?
if (/\d/.test(key)) {
currentVal += key;
return key;
}
}
function eq() {
// = key?
if (currentOper != "=") {
currentTotal = op(currentTotal, currentOper, Number(currentVal));
currentOper = "=";
currentVal = "";
return formatTotal(currentTotal);
}
return "";
}
function operator(key) {
// multiple operations in a series?
if (currentOper != "=" && currentVal != "") {
// implied '=' keypress
eq();
} else if (currentVal != "") {
currentTotal = Number(currentVal);
}
currentOper = key;
currentVal = "";
return key;
}
function op(val1, oper, val2) {
var ops = {
// NOTE: using arrow functions
// only for brevity in the book
"+": (v1, v2) => v1 + v2,
"-": (v1, v2) => v1 - v2,
"*": (v1, v2) => v1 * v2,
"/": (v1, v2) => v1 / v2,
};
return ops[oper](val1, val2);
}
}
var calc = calculator();
useCalc(calc, "4+3="); // 4+3=7
useCalc(calc, "+9="); // +9=16
useCalc(calc, "*8="); // *5=128
useCalc(calc, "7*2*3="); // 7*2*3=42
useCalc(calc, "1/0="); // 1/0=ERR
useCalc(calc, "+3="); // +3=ERR
useCalc(calc, "51="); // 51

That's it for this book, congratulations on your achievement! When you're ready, move on to Book 3, Objects & Classes.

Original Source

You can read original author source from here

  1. Math.js: isPrime(..), https://github.com/josdejong/mathjs/blob/develop/src/function/utils/isPrime.js, 3 March 2020.↩
Edit this page